Oral Presentation International Solvent Extraction Conference 2025

Slope analysis is used worldwide to rapidly estimate the stoichiometry of the major complex formed during solvent extraction. Still, many authors reported failures of this method. This presentation aims to highlight some pitfalls of the method, illustrated by experimental cases.

A usual mononuclear complex formation reaction is M^p+ + pX^- + nL = (MX_pL_n) for monovalent anions. The origin of the slope method is the correlation between the distribution ratio D_M and the formation constants K_n.

D_M = [M]_org/[M]_aq         K_n = {MXL_n}/({M^p+}{X^-}^p{L}ⁿ) = γ_n[MXLn]/(γ_M[M^p+]{X^-}^p{L}ⁿ)

Most often, the aqueous metal concentration equals that of the cation M^p+ : [M]_aq=[M^p+]. Provided that the diluent itself does not extract the metal, the organic concentration is equal to the sum of the concentrations of the complexes: D_M={M^p+}{X^-}^pΣK_i{L}ⁱ/γ_i/[M^p+]=γ_M{X^-}^pΣK_i{L}ⁱ/γ_i

Moreover, the slope method considers that the activity coefficients in the organic phase are equal to 1 and that only one species contributes to most of the extraction, hence the final equation D_M=γ_M{X^-}^pK_n[L]ⁿ, becoming log(D_M)=log(γ_M{X^-}^pK_n)+nlog([L]). In most publications, [L]=[L]_init with little to no justification, although this condition holds true only at low metal loading and without any other competitive cations.

This rather long list of conditions required to correctly implement the slope method induces failures or confusing results when they are not met. Below are some examples that we encountered in our lab.

• Competition with other cations: H⁺ example

The distribution ratio decreases in the presence of other cations due to their competitive extraction by the ligand. In acidic conditions, the ligand often protonates, associated with the co-extraction of counter-anions to keep the charge balanced. The easiest quantitative method to account for this competition is additional complex formation reactions: aH⁺ + aX^- + L = (H_aX_aL) where the range of a depends on the number of protonation sites of the ligand. If the concentration of the competitor is high enough, its extraction decreases the concentration of free ligand that can bind the targeted element, hence a decrease in distribution ratios. The free ligand concentration should thus be adjusted to plot correct values for the slope method.

• Non linearity of the log-log plot

A second commonly reported effect is a deviation from linearity when increasing the ligand concentration. It can be modelled by considering changes in ligand concentration due to the volume variation when extracting large amounts of water, electrolytes and/or acid and by estimating the organic activity coefficients (e.g. with the Scatchard–Hildebrand–Scott simple empirical model).

• Co-extraction of cations in the same complex

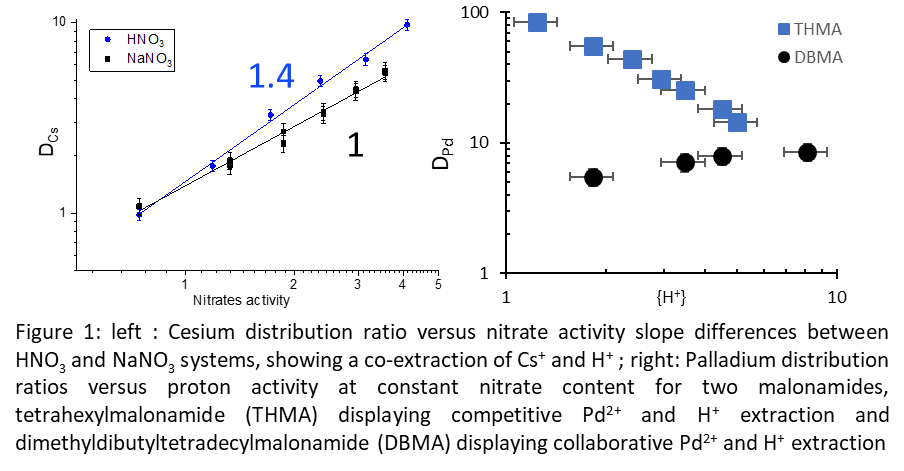
Ligands owning more than one coordination sites are able to complex several metals. The examples in Figure 1 highlight H⁺ co-extraction with Cs and Pd. The presence of (MH_aX_(p+a)L_n) species induces discrepancies in the slope method performed at low and high nitric acid concentrations, as the main species usually differ.

• Dependence on metal concentration

For mononuclear complexes, the distribution ratio is independent from metal concentration until the saturation of the ligand is reached. However, if complexes contain more than one cations, the distribution ratio increases with metal content, as shown in Figure 2.

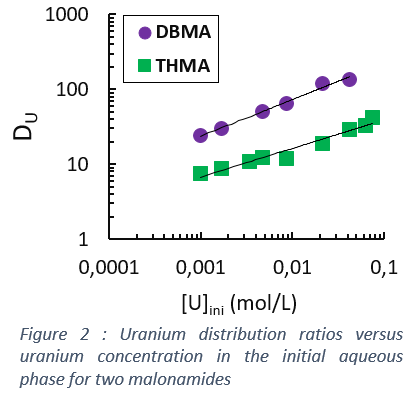
The reaction is then mM^p+ + mpX^- + nL = (M_mX_mpL_n), leading to D_M=Σ_m{M^p+}^m{X-}^mpΣ_iK_i{L}ⁱ/γ_i/[M^p+] and to a dependence of the slope on [M^p+]: [M^p+] decreases at higher extraction yields, thus decreasing with increasing ligand concentration.

In conclusion, the slope method was developed at a time when calculation tools were insufficient to accurately fit data without simplified equations, but these simplifications induce errors in many cases. Nowadays, activity coefficients and power fittings are easily and rapidly computed, allowing for more accurate and complete models able to address most shortcomings of the slope method by considering all formed complexes instead of only one.